Undersanding Electrical Principles And Simple Circuits

Before beginning, I should note that this blog makes the assumption that the vehicle you own has a 12 volt negative ground charging system. That is, the vehicle is equipped with a 12 volt battery and its negative terminal is connected to the vehicle chassis. If you own a vehicle with a 6-volt or even a positive ground charging system, the theory still applies but the specifics do not.

The objective here is to provide a foundation for the rest of the book. Everything you need to know is explained so that you have a firm understanding of basic automotive electronics. Every other blog post in this blog is written on the assumption that you've read and understood this one.

High Current/Low Voltage

The single most important thing to keep in mind when working on a vehicle's electrical system is safety. Unlike the electrical system of your home, automotive electrical systems are low voltage, so there is little if any danger from shock. In addition, an automotive electricakl system can deliver incredibly high currents--far in excess of the 15 ampsavailable at a typical outlet in your livingroom. Finally, this current is direct current or DC versus the alternating current or AC found in your home.

• Automotive Electrical--Low Voltage / High Current (DC)
• Residential  Electrical--High Voltage / Low Current (AC)

I assume that if you're reading this post, then you've experienced first hand the results of a short circuit in an automobile. They can cause extreme damage quite quickly!

I need to address two laws right away. A good friend once told me, "They're laws, not just really good ideas." Well put. The two laws that are paramount to understand for automotive wiring projects and nearly all electrical projects are Ohm's Law and Kirchhoff's Law.

Ohm's Law



Ohm's law is generally considered the foundation of electronics. Named after the person that first defined it, George Ohm, Ohm's law simply states the relationship between voltage (V), current (I), and resistance (R).

Ohm's law triangle 

In circuit analysis, three equivalent expressions of Ohm's law are used interchangeably:

Voltage

• Difference in potential
• Measured in volts
• Typically expressed as V or E in mathematical formula

Current

• Flow of electrons
• Measured in amperes (can be abbreviated as amps)
• Typically expressed as I in mathematical formula

Resistance

• Opposition to the flow of electrons
• Measured in ohms ( interchangeable with the  symbol )
• Typically expressed as R in mathematical formula

Voltage is that which causes current to flow. Resistance is anything that impedes the flow of current. The higher the resistance, the higher the voltage required to allow a given amount of current to flow. This relationship between voltage, current, and resistance is expressed as:  I=V/R

If you know any two of the above, you can solve for the third. Using a little algebra, you can re-arrange this formula to get the following formulas to aid in solving for the unknown :
V=IxR
R=V/I

Fortunately, the voltage available in a vehicle is somewhat fixed and typically is 12--12.6 VDC with the vehicle off and 13.0---14.4 VDC with the vehicle running.

Now that you know Ohm's Law, let's put it to work to determine how much resistance an electronic fuel pump has if it requires 10 amps of current at 12 Volts.

R=V/I
R=12 volts / 10 amps
R=1.2

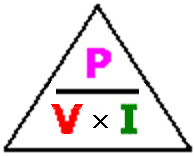
The Power Formula

The power formula simply states the relationship between power, current and voltage. Power is an expression of work and is expressed in watts. Power is the product of current and voltage and the relationship is expressed as: P=IxV

Again, if you knowe any two, you can solve for the third. Once again, let's use a little algebra to re-arrange this formula to aid in solving for the unknown:

I=P/V
E=P/I


Now that you know the Power Formula, let's use it to determine how much power the electronic fuel pump I spoke of above consumes:

P=IxV
P=10amps x 12volts
P=120 Watts

An easy way to put the idea of power into perspective is to understand the simple incandescent light bulb. For example, a bulb rated 60 watts consumes 60 watts of power to light the filament within the bulb. Not all of the power across the filament can be converted to light --- some of the 60 watts the bulb consumes is converted to heat. This is why the bulb gets hot in use. The same applies to electronic circuits in all automobiles.

In a simple circuit, a certain amount of power is dissipated across the load. The remaining power is dissipated into heat in the wiring, switch(es), and connections. By minimizing the amount of power burned up into heat, we can get more power to the load.

Combinations
Many times, you need to solve problems that neither Ohm's Law or The Power Formula addresses directly. However, they can provide the solution whern you combine them via substitution. For examle : P=V^2/R

This formula would allow us to solve for power if we know voltage and resistance, but not current. How did we deytermine this? Simple, Ohm's Law tells us that I=V/R, so we can substitute V/R for I in the Power Formula:

P=IxV (Recall that I=V/R)
P=(V/R)xV
P=V^2/R

Likewise, we can solve for power if wee know curtrent and resistance but not voltage the same way:

P=IxV (Recall that V=IxR)
P=Ix(IxR)
P=I^2R